Matrix Inverse using Optimizer

AnkitGupta

In the following article, we will discuss how to use Anaplan Optimizer to compute Matrix Inverse. Matrix Inverse as a functionality can be used to solve a Multi Linear Regression Problem in Anaplan. Using Matrix Inverse, we are going to solve the following Multi Linear Regression equation:

Y = b0 + b1x1 + b2x2 + b3x3 + b4x4 + b5x5 + b6x6 + b7x7 + b8x8

• x1 to x8 are called Independent Variables.
• Y is called a dependent variable whose value we are trying to find.
• b0 to b8 are called coefficients for the constant and the independent variables (x1  to x8).

Y = X * B

X(T)*Y = (X(T)*X) * B

Taking X(T) * X to other side

(X(T) *X)-1 X(T)*Y = B

Multi Linear Regression can be used to find out the factors which are impacting your dependent variable (ex: Causal Forecasting).

You can use the following steps to calculate Matrix Inverse in Anaplan using optimizer and then use that to complete your Multi Linear Regression problem.

Theory used to solve Matrix inverse is M* M^-1 = I.

Matrix * Matrix inverse = Identity Matrix.

We know the values of Matrix and Identity Matrix, and we are going to use Optimizer to compute the variable which is our Matrix Inverse. This trick is going to help us compute MMULT.

And Optimizer will do the heavy lifting for us and compute Matrix Inverse for us.

The following are the steps:

Lists

Create four lists I9x9 (Rows), J9x9 (Columns), K9x9 (Dummy List), Item and Populate them as follows:

• R1 to R9 as list members in I9x9  -> Make a number property to hold row number (R1 =1...R9=9)
• C1 to C9 as list members in J9x9 -> Make a number property to hold column number (C1 =1...C9=9)
• K1 to K9 as list members in K9x9 -> Make a number property to hold column number (K1 =1...K9=9)
• Item-1 to Item-xxx as list members in Item list (These are number of items for which we want to calculate the matrix inverse)
• Include Top Level for all the above lists

Module

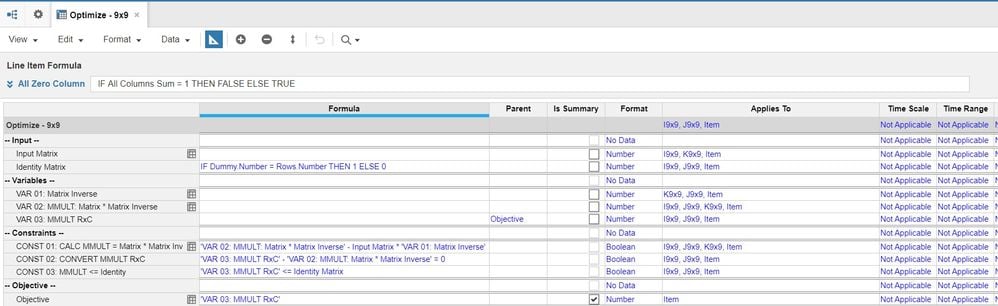
Create a Module with the following line items:

-- Input --

Input Matrix -> This is Input Matrix for Matrix

Identity Matrix -> If row number=column number Then 1 else 0

-- Variables --
VAR 01: Matrix Inverse -> This is the Matrix Inverse Optimizer is solving for
VAR 02: MMULT: Matrix * Matrix Inverse -> Intermediate variable to calculate Matrix *Matrix Inverse
VAR 03: MMULT RxC -> Changing Dimensions of the MMULT result above from IxJxK to IxJ

-- Constraints --
CONST 01: CALC MMULT = Matrix * Matrix Inverse -> Calculating Matrix * Matrix Inverse
CONST 02: CONVERT MMULT RxC -> Changing dimension of MMULT result above from IxJxK to IxJ
CONST 03: MMULT <= Identity -> Constraining VAR 03: MMULT RxC<= Identity Matrix

-- Objective --
Objective -> Maximizing VAR 03: MMULT RxCso VAR 03: MMULT RxC = IDentity Matrix whenever a Matrix inverse exists (If Determinant of a Matrix is 0 then Matrix inverse does not exist!)

Formula and Dimensions

Use this to configure the formulas and dimensions for these line items. 

 

 

 

 

 

 

 

 

 

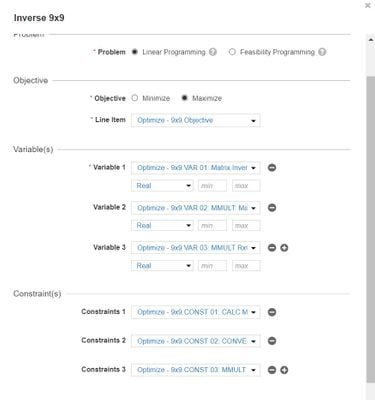
Optimizer

Use this to configure Optimizer

Once you run the optimizer then you will be able to see the value of Matrix inverse in VAR 01: Matrix Inverse.

 

 

 

 

 

 

 

 

 

 

Please Note: While testing the solution, ensure that your Input Matrix has numbers put in such a way that its Determinant is not Zero (because a matrix with zero determinant will not have an Inverse)

Contributing authors: Vinay Varadaraj Mirajkar and Anne-Julie Balsamo.

MaciejD

Hello AnkitGupta,

Very interesting approach to use the Optimiser! Could you explain further what you are doing after having the Inverse Matrix calculated? I mean how to technically proceed to finally solving the Multi Linear Regression Problem?

Best regards,

Maciej