How to traverse hierarchies: The power of loops
Introduction
Whenever you use a hierarchy, there will often be times when you are required to seek specific information which will necessitate some way to traverse the nodes and map out their connections. What you seek may be a list entity, a specific value, or a unique identifier, and this can become complicated if the hierarchy in question is a ragged or many to many.
Hierarchical goal seeking
No matter the relationship between two nodes, whether parent/child or variable many-to-many connections, you will need a way to traverse the mapping. The question when simplified becomes "when I’m at X, how do I reach Y?"
And this question is the same for both a basic parent/child relationship and for many to many relationships:
The answer to this (if a connection exists) is iterative searching. This can also be compared to goal seeking, where the goal lies at the end of the node connections rather than a targeted value that you are trying to calculate. This method also allows you to identify every connection along the route, which can be useful for non-standard filtering procedures.
Building the engine
If we take a standard goal seeking model, first we need to identify a target. In the example below we’ll have this as a user driven selection from a ragged hierarchy. What we want to find is all connected child nodes of the users’ choice:
Once a choice has been made, we can feed this into our iteration module:
The time setting when paired with a PREVIOUS() formula can be used to imitate a loop within our line item ‘Level Result’:
This allows us to reference our previous results within the next cycle. In this example, we’re using the Ragged List as a dimension then using the loop to cycle through all its connected parent nodes. If during this cycle we find the node we’re looking for, we tag the current list item with our Boolean flag.
When the result is pulled into a module without time (via a TIMESUM() formula), we can check that our goal seek has worked as intended:
For this simple example, a similar effect can be achieved via an attribute module which breaks out all parent hierarchy levels with a direct reference to the level being searched for. However, by using the iteration method, we can be more flexible in our choices and adapt quickly to any change in the hierarchy’s structure. I would also recommend isolating your iteration to its own time range so that you may adjust it as needed without model impact.
Filtering
Now that we have a working search loop, we can expand our use case into scenarios that may have otherwise proved difficult without an iterative mechanism. A common requirement is dynamic filtering based on user selection. When dealing with a large hierarchy, users will often need to look at chunks of the list in isolation, removing noise that can create overly cluttered outputs. In our current example a user has selected Level 4b, and we can potentially filter on all nodes below this point. To illustrate this, we have the following data output module:
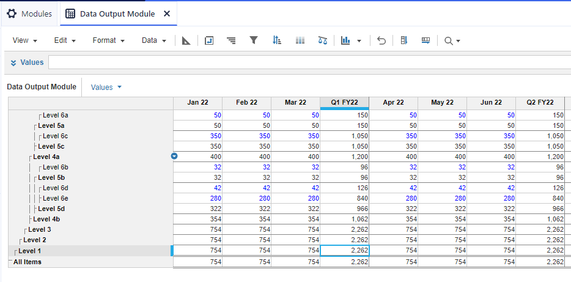
Which can now be filtered like so:
This works for our simple list; however, when dealing with a much larger hierarchy, you may wish to isolate your results with a limiter based on how many iterative steps you are away from the original target. To achieve this, we must know at what level our target sits in the hierarchy and the users desired distance range. First we’ll find the level of our users target by adding some new line items to our iteration example:
The ‘Current List Level’ can be contained within an attribute module, but for our example I’ve condensed our module sources. ‘Count w/ Min Summary’ is a minor augmentation to our loop, with this in place we’ll have an iterating number to work with no matter the size of our list. ‘List Level Count’ will isolate the number of loops needed to reach our current list item. Finally, ‘Level of Search Item’ will compare our users target with the level we’re looking at and supply a numerical answer for the level we’re looking for. Next, we can add a user-controlled range to our input module, as well as an identifier of what list level their current search resides at:
Next we will create a new filtering module using the hierarchy we’re searching through so that we can collect our data:
With this module we’ve brought through our original loop results within the line item ‘Initial Loop Results inc Parents’ but now we’ve allowed for any parents of the target to be flagged by setting the summary option to ‘Any’. This is to create an overarching limitation to our secondary search results data range.
Under ‘List Levels’ we’ve used a TIMESUM() to bring in our list level count, and then we've derived the distance from our users target within the line item ‘Distance from search target’ using this formula:
Then finally, we’ve combined our logic together to create our new filter flag:
This will allow a user to have dynamic control over the items flagged within the hierarchy and, like before, we can now use our Boolean to filter our data module:
Common missteps
This process is relatively light weight and quick to setup; however, this method isn’t common practice for most model builders. A regular misstep can be a lack of clarity for future users when designing the process. It’s unlikely that a front end user will need to see the details of the loop; however, future model builders who may not be familiar with this process should not feel lost upon review of the steps. To ensure this is the case, break out each step in the design and clearly label what the calculations purpose is (employ the module notes and any documentation storage you have for more complex scenarios).
When using the dynamic filtering, check whether any data values will also need limiting. Now that you’re giving users control of the data displayed you need to ensure that only the list items selected provide data for aggregation else your reporting will not reconcile. This can be done using the Boolean flags created throughout the process.
Summary
At its core, a well-structured loop can be applied to countless scenarios. If we have a way to identify our search parameters, we can feed anything we require into our engine. Then once we have mapped the path, we can send data across it. In this simple example we’ve merely identified the path we wish to take, but with further iterations and more complicated use cases, we can pass information along this freshly charted path and create relationships between nodes that would have otherwise been extremely difficult to identify.
Comments
-
Thank You Adam.
A well written article which is very valuable.
Ravinder.
0 -
Nice article, Adam. Thanks much for the inspiration! I'll give this a go the next time I use a ragged hierarchy
0 -
Interesting, hope to try this out for ragged org hierarchy. Thanks for sharing.
Asslam
0 -
I have finally been able to review your article in detail and recreate the outputs.
However, while I can see the possibility of applying in theory I am struggling to see how to apply this to other use cases. In the first example you provide above I would rather use an ISANCESTOR function which could be used to identify decedents. While this can not be used to search a range of targets from an input I am not sure where I would need to apply this.
Therefore, more examples of where applying a loop structure would be greatly appreciate so I can visualise other applications.
0 -
Hi Chris,
The ISANCESTOR logic is quite limiting, the purpose of establishing a loop is to enable more complex search functionality and data traversal.
For example, if you're attempting to pass data throughout a many to many positional structure for bespoke filtering you're going to have to calculate connections in patterns that you don't have a standard hierarchy for and users will want to select data points at any level and filter their connections in a simple way. Understanding the premise of looping can help with this, as you'll be able to iterate through your results to locate a target of the users choice.
0
